Resolución de Integrales por Cambio de Variable
Consiste en igualar una parte del integrando a una nueva variable, por ejemplo u, llamada variable auxiliar. Luego de esto, se debe calcular la derivada de la variable auxiliar y realizar las operaciones necesarias, para que ni en el integrando ni en el diferencial, aparezca alguna expresión en términos de la variable original. A esto se le denomina cambio de variable (Cambio de variable).
Luego de hacer efectivo el cambio de variable , por lo general, se obtienen integrales más sencillas que la original, las cuales se resuelven aplicando lo aprendido en el método anterior. Por esta razón, es necesario que el lector haya estudiado detalladamente dicho método puesto que en la solución de los ejemplos de esta parte de la obra, no se incluye una explicación específica de este contenido que ya debe ser parte de sus redes conceptuales.
Es importante señalar que el resultado de la integración, debe estar en función de las variables originales por lo que se acostumbra a emplear el término “devolviendo el cambio de variable” para reseñar el proceso mediante el cual la variable auxiliar desaparece de la respuesta definitiva
Método
Queremos resolver la siguiente integral
- Buscamos un cambio de variable: g(u) = x (o bien u = g-1(x) )
- Derivamos en la igualdad:

- Sustituimos en la integral
- x por g(u)
- dx por

- Calculamos la integral con la nueva variable.
- Deshacemos el cambio de variable.
Cambios de variables útiles
EJEMPLO:










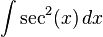 .
.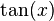 es
es 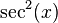 . Por tanto:
. Por tanto: