Como un conjunto, que contiene los miembros
(también llamados elementos o términos), y el número de términos (posiblemente
infinita) se llama la longitud de la secuencia. A diferencia de un conjunto, el
orden importa, y exactamente los mismos elementos pueden aparecer varias veces
en diferentes posiciones en la secuencia. Una secuencia es una discreta
función. Por ejemplo, (C, R, Y) es una secuencia de letras que difiere de (Y, C,
R), como las cuestiones de pedido. Las secuencias pueden ser finitos, como en
este ejemplo, o infinita, como la secuencia de todos, incluso positivos enteros
(2, 4, 6,…). Secuencias finitos se conocen como cadenas o palabras y secuencias
infinitas como los arroyos. La secuencia vacía () se incluye en la mayoría de
las nociones de secuencia, pero pueden ser excluidos en función del contexto.
CRITERIO DE D'ALEMBERT
Sea una serie  , tal que ak > 0 ( serie de términos positivos).
, tal que ak > 0 ( serie de términos positivos).
Si existe
con 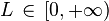 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:
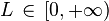 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que:- si L < 1, la serie converge.si L > 1, entonces la serie diverge.si L = 1, no es posible decir algo sobre el comportamiento de la serie.En este caso, es necesario probar otro criterio, como el criterio de Raabe.
Sea una serie  , tal que ak > 0 (serie de términos positivos). Y supongamos que existe
, tal que ak > 0 (serie de términos positivos). Y supongamos que existe
 , tal que ak > 0 (serie de términos positivos). Y supongamos que existe
, tal que ak > 0 (serie de términos positivos). Y supongamos que existe![\lim_{k \rightarrow \infty} \sqrt [k] {a_k}=L](http://upload.wikimedia.org/math/9/f/9/9f9c8260d0ee84308bde583dc2ca8991.png) , siendo
, siendo 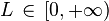
- Entonces, si:L < 1, la serie es convergente.L > 1 entonces la serie es divergente.L=1, no podemos concluir nada a priori y tenemos que recurrir al criterio de Raabe, o de comparación, para ver si podemos llegar a alguna conclusión.
No hay comentarios:
Publicar un comentario